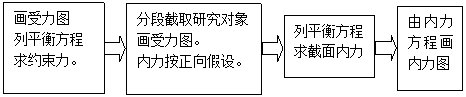‍用截面法作梁的内力图

如第四章所述，用截面法求构件各截面内力的一般步骤是：先求出约束力，再用截面法将构件截开，取其一部分作为研究对象，画出该研究对象的受力图；截面上的内力按正向假设，由平衡方程求解。在第四章中不仅已经讨论了用截面法求构件内力的一般方法，还给出了构件横截面上内力的符号规定。下面将通过若干例题，进一步讨论如何利用截面法确定平面弯曲梁横截面上的内力。

解：1）求固定端约束力。

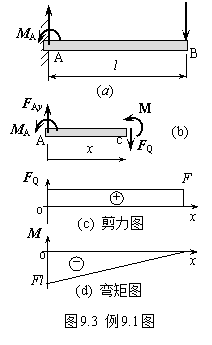
固定端A处有三个约束力，但因梁上无x方向载荷作用，故F_Ax=0；只有F_Ay、M_A如图所示。列平衡方程有：
      ∑M_A(F )=M_A-Fl=0        ∑F_y=F_Ay-F=0    

得到： F_Ay=F； M_A=Fl

2）求截面内力。

在距A为x处将梁截断，取左段研究，截面内力按正向假设，如图9.3(b)所示。

在0≤x〈l内，有平衡方程：

∑F_y=F_Ay-F_Q=0    

 ∑M_C(F )=M_A+M-F_Ayx=0   

得到： F_Q=F； M=-F(l-x)

注意，在x=l的右端B点，因为梁处于平衡，B点右边截面之内力均为零。梁二端点外内力为零，以后将不再赘述。

    3) 画内力图。在0≤x≤l内，剪力F_Q=F，剪力图为水平线，如图9.3(c)所示。弯矩M随截面位置线性变化；当x=0时，M=-Fl；x=l时，M=0；弯矩图为连接此二点的直线，如图9.3(d)所示。此悬臂梁在固定端A处弯矩值最大。

解：1）求约束力。注意固定铰A处F_Ax=0，故梁AB受力如图所示。列平衡方程有：

         ∑M_A(F )=F_By(2a+b)-Fa-F(a+b)=0   

∑F_y=F_Ay+F_By-2F =0    

       得到： F_Ay=F_By=F；                 

2）求截面内力。

0≤x₁〈a；左段受力如图9.4(b)。

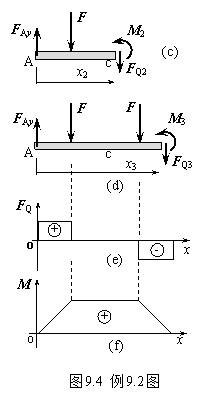
由平衡方程有：

 ∑F_y=F_Ay-F_Q1=0；→  F_Q1=F_Ay=F；

∑M_C(F )=M₁-F_Ayx₁=0  → M₁=Fx₁

a≤x₂〈a+b；左段受力如图9.4(c)。

由平衡方程有：

F_Q2=F_Ay-F=0

M₂=F_Ayx₂-F(x₂-a)=Fa  

a +b≤x₃〈2a+b；左段受力如图9.4(d)。

 由平衡方程有：

 F_Q3=F_Ay-2F=-F

M₃=F_Ayx₃-F(x₃-a)-F(x₃-a-b)=F(2a+b)-Fx₃

注意在x=2a+b的右端B点，截面之内力（F_Q、M）必然回至零。

3) 画内力图。

剪力图如图9.4(e)所示。注意在a≤x≤a+b段内，F_Q=0。

在0≤x〈a和a+b≤x〈2a+b二段内，弯矩M随截面位置x线性变化；在x=0和x=2a+b二端，M=0；二集中力作用处，即x=a和x=a+b处，有M=Fa；在a≤x〈a+b段内，M=Fa；故弯矩图如图9.4(f)所示。

梁在a≤x〈a+b段内，只有弯矩，没有剪力，这种情况称为纯弯曲。

用截面法作梁的内力图实例‍

解：1) 求反力。梁受力如图9.6(a)所示，列平衡方程有：

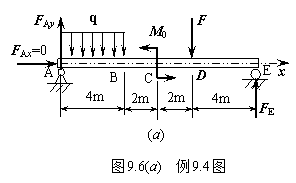
   ∑F_x=F_Ax=0

   ∑M_A(F)=12F_E+M₀-8F-2×4q=0 

   ∑F_y=F_Ay+F_E-F-4q=0      

   解得：

F_Ay=49kN；  F_E=32kN

   2) 求截面内力。

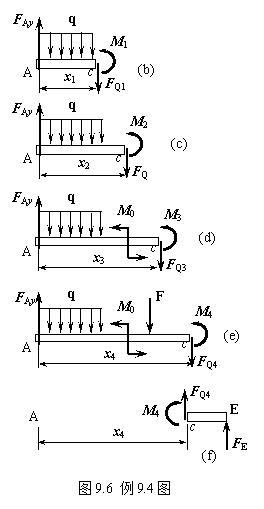
求内力时，应在载荷发生变化处分段研究。以A为原点，建立坐标如图9.6(a)。则应在B、C、D处分段。

AB段（0≤x₁<4m）：在任一x₁处将梁截断，取左端研究，受力如图9.6(b)。注意到由∑F_x=0已给出轴力为零，故截面1上只有剪力和弯矩。

列平衡方程有：

∑F_y=F_Ay-qx₁-F_Q1=0                    

→  F_Q1=49-9x₁

∑M_c(F)=M₁+qx₁²/2-YAx₁=0      

→   M₁=49x₁-4.5x₁²

    注意力矩方程均是以截面形心c为矩心写出的，如此可直接得到截面弯矩。

BC段(4≤x₂<6m)：受力如图9.6(c)所示。同样有：

∑F_y=F_Ay-4q-F_Q2=0     →    F_Q2=F_Ay-4q=49kN-9(kN/m)´4m=13kN

∑M_c(F)=M₂+4q(x₂-2)-F_Ayx₂=0    →  M₂=13x₂+72(kN·m)

 CD段（6≤x₃<8m）：受力如图9.8(d)，有：

∑F_y=F_Ay-4q-F_Q3=0    →   F_Q3=13kN

∑M_c(F)=M₃+4q(x₃-2)+M₀-F_Ayx₃=0  →  M₃=13x₃+24(kN·m)

DE段（8≤x₄<12m）：受力如图9.6(e)，有：

 ∑F_y=F_Ay-4q-F_Q4-F=0    →    F_Q4=-32kN

∑ M_c(F)=M₄+4q(x₄-2)+M₀+F(x₄-8)-F_Ayx₄=0   → M₄=384-32x₄(kN·m)

由截面法求内力时，无论取左右哪一端研究都应得到相同的结果。如在DE段截取右端研究，注意截面内力仍按正向假设，受力如图9.6(f)所示，有：

∑F_y=F_Q4+F_E=0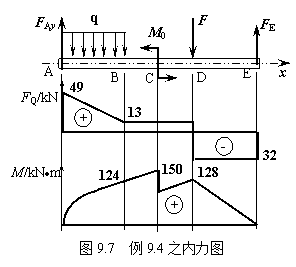  

∑M_c(F)=-M₄+F_E(12-x₄)=0

同样得到：

F_Q4=-F_E=-32kN；

M₄=384-32x₄ (kN·m)

值得注意的是，同一截面上的内力，如图9.6(e)与图9.6(f)中的截面4，在物体不同的部分上互为作用力与反作用力，故应有相反的指向（如图中F_Q4、M₄）。前面给出的内力符号规定可使二者有同样的表达。

本例分四段给出了各截面的剪力方程和弯矩方程，依据这些内力方程画出的剪力图和弯矩图，如图9.7所示。注意观察梁上作用载荷变化处，剪力图、弯矩图的变化。

综上所述，用截面法求内力的一般方法是：